箱线图
一、箱线图介绍:
箱线图(Box-plot)又称为盒须图、盒式图或箱型图,是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。在各种领域也经常被使用,它主要用于反映原始数据分布的特征,还可以进行多组数据分布特征的比较。箱线图的绘制方法是:先找出一组数据的上限值、下限值、中位数(Q2)和下四分位数(Q1)以及上四分位数(Q3);然后,连接两个四分位数画出箱子;再将最大值和最小值与箱子相连接,中位数在箱子中间。
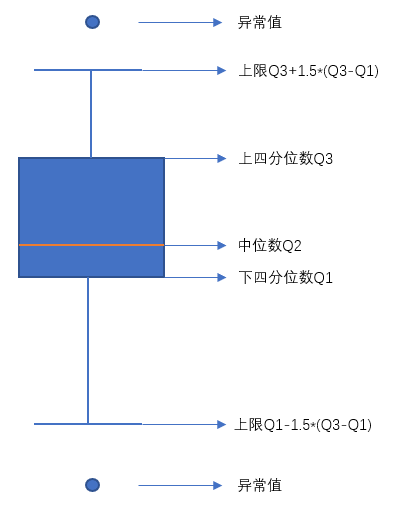
中位数:把数据按照从小到大的顺序排序,然后最中间的那个值为中位数,如果数据的个数为偶数,那么就是最中间的两个数的平均数为中位数。
上下四分位数:同样把数据排好序后,把数据等分为4份。出现在25%位置的叫做下四分位数,出现在75%位置上的数叫做上四分位数。但是四分位数位置的确定方法不是固定的,有几种算法,每种方法得到的结果会有一定差异,但差异不会很大。上下限的计算规则是:
IQR=Q3-Q1
上限=Q3+1.5IQR
下限=Q1-1.5IQR
二、使用matplotlib绘制箱线图:
在matplotlib中有plt.boxplot来绘制箱线图,这个方法的相关参数如下:
x:需要绘制的箱线图的数据。notch:是否展示置信区间,默认是False。如果设置为True,那么就会在盒子上展示一个缺口。sym:代表异常点的符号表示,默认是小圆点。vert:是否是垂直的,默认是True,如果设置为False那么将水平方向展示。whis:上下限的系数,默认是1.5,也就是上限是Q3+1.5IQR,可以改成其他的。也可以为一个序列,如果是序列,那么序列中的两个值分别代表的就是下限和上限的值,而不是再需要通过IQR来计算。positions:设置每个盒子的位置。widths:设置每个盒子的宽度。labels:每个盒子的label。meanline和showmeans:如果这两个都为True,那么将会绘制平均值的的线条。
示例代码如下:
data = np.random.rand(100)*100
# 添加两个异常值
data = np.append(data,np.array([-100,100]))
plt.boxplot(data,meanline=True,showmeans=True)
效果图如下:
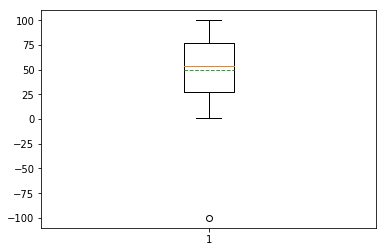
如果有多组数据绘制箱型图,才能更好的提现出箱型图的优势。
假如我们想要获取奥林匹克运动会上不同国家运动员的身高情况,那么可以把每个国家的运动员身高数据绘制成一个箱线图,然后进行对比。示例代码如下:
athletes = pd.read_csv("athlete_events.csv")
# (中国CHN,日本JPN,韩国KOR),(埃塞俄比亚ETH,肯尼亚KEN,尼日利亚NIG),(美国USA,加拿大CAN,巴西BRA),(英国GBR,法国FRA,意大利ITA)
countries = {
'CHN':'中国',
'JPN':"日本",
'KOR':'韩国',
'USA':"美国",
'CAN':"加拿大",
'BRA':"巴西",
'GBR':"英国",
'FRA':"法国",
'ITA':"意大利",
'ETH':"埃塞俄比亚",
'KEN':"肯尼亚",
'NIG':"尼日利亚",
}
dfs = []
for code in countries.keys():
df = athletes[(athletes['NOC'] == code)&(athletes['Age']>18)]['Height'].dropna()
dfs.append(df)
font = font_manager.FontProperties(fname=r"C:\\Windows\\Fonts\\msyh.ttc",size=14)
plt.figure(figsize=(20,5))
plt.boxplot(dfs,showmeans=True,meanline=True,labels=countries.values())
plt.xticks(range(1,13),countries.values(),fontproperties=font)
plt.ylabel("身高(cm)",fontproperties=font)
plt.title("奥林匹克运动员身高箱线图",fontproperties=font)
效果图如下:
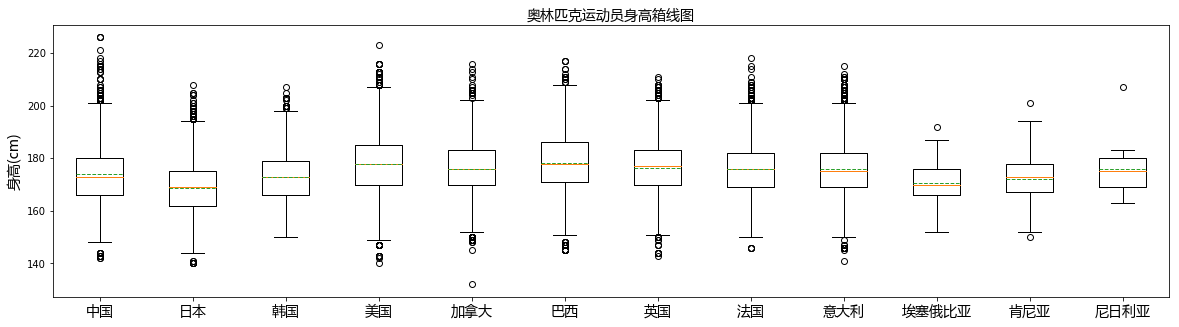
三、箱线图的应用场景:
- 直观明了地识别数据中的异常值。
- 利用箱线图判断数据的偏态。
- 利用箱线图比较几批数据的形状。
- 箱线图适合比较多组数据,如果知识要看一组数据的分布情况,建议使用直方图。
